摘 要:將環狀燃氣管網布置優化問題轉換為旅行商問題,采用蟻群算法進行求解,列舉了算例。
關鍵詞:環狀燃氣管網 布置優化 旅行商問題 蟻群算法
Layout Optimization of Loop Gas Pipe Network Based on Ant Colony Algorithm
Abstract:The layout optimization problem of loop gas pipe network is converted into a traveling salesman problem,and solution is performed by ant colony algorithm.The calculation examples are enumerated.
Keywords:loop gas pipe network;layout optimization;traveling salesman problem;ant colony algorithm
在設計燃氣管網時,設計人員通常根據經驗確定布置形式,這使得管網的合理性有待探討。此外,國內外學者對枝狀管網的布置優化問題研究較多,對環狀管網的布置優化研究較少[1-5]。本文將環狀燃氣管網布置優化問題轉換為旅行商問題(Traveling Salesman Problem,簡稱TSP),采用蟻群算法進行求解。
1 TSP
TSP是圖論領域中著名問題之一。形象地說,TSP是指一名旅行售貨員從一座城市出發,訪問每座城市恰好一次,再回到出發城市,最終使得旅費最低。對于燃氣管網,將調壓站、調壓裝置視為TSP中的“城市(節點)”,節點之間敷設的燃氣管道造價視為“旅費”,要求從起始節點出發,訪問剩余的每個節點恰好一次,再回到起始節點,要求燃氣管道造價最低。由此可知,環狀燃氣管網的布置優化問題與TSP十分相似,因此可以將環狀燃氣管網布置優
化問題轉換為TSP。
2 蟻群算法
蟻群算法(Ant Colony Algorithm,ACA)是1991年M.Dorigo提出的一種智能算法。該算法來源于螞蟻種群的覓食行為,其本質是一個龐大的智能體系,具有很強的容錯性及并行計算能力,可與其他算法無縫銜接。
2.1 蟻群算法的數學模型
為了方便討論,設bi(t)表示t時刻位于節點i的螞蟻數量,則螞蟻總數量m的表達式為:
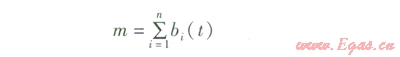
式中m——螞蟻總數量
n——節點總數
n個節點的集合為:
C={c1,c2,c3,…,cn}
式中C——n個節點的集合
c1…cn——集合C中的元素
節點i與j路徑長度的集合為:
L={lijúci,cjÌC}
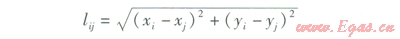
式中L——集合C中節點i與j路徑長度的集合
lij——節點i與j路徑長度,m
xi、yi——節點i在二維坐標系(xOy)中的坐標
xi、yi——節點歹在二維坐標系(xOy)中的坐標
t時刻節點i與j路徑上殘留信息量集合G的表達式為:
G={tij(t)ú ci,cj,ÌC}
式中G——t時刻節點i與j路徑上殘留信息量集合
tij(t)——t時刻節點i與j路徑上的殘留信息量,在初始時刻各條路徑上殘留信息量相等
螞蟻k(1,2,3,…,m)的運動方向是根據各條路徑上的殘留信息量來確定的,t時刻螞蟻k由節點i轉移到節點j的狀態轉移概率為:

式中Pij(t)——t時刻螞蟻k由節點i轉移到節點j的狀態轉移概率
a——信息啟發式因子,表示軌跡的相對重要性
hij(t)——啟發函數
b——期望啟發式因子,表示能見度的相對重要性
A——螞蟻k下一步允許選擇的節點集合,A={C-B},B表示螞蟻k已經走過的節點集合
需要注意的是,在每只螞蟻走完一步或者完成對所有n個節點的遍歷后,要對殘留信息進行更新處理,否則過多的殘留信息會淹沒啟發信息。因此,在螞蟻經過一個節點或經過所有節點完成一個循環所需的時間T后,即t+T時刻在節點i與j路徑上的殘留信息量tij(t+T)可按以下規則進行調整:
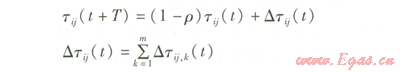
式中tij(t+T)——t+T時刻在節點i與j路徑上的殘留信息量
r——信息素揮發系數,取值范圍為[0,1)
Dtij(t)——本次循環中節點i與j路徑上的信息素增量,初始時刻為0
Dtij,k(t)——本次循環中第k只螞蟻在節點i與j路徑上的信息素增量
M.Dorigo提出了3種不同的信息素更新模型,分別為:Ant-Cycle模型、Ant-Quantity模型、Ant-Density模型,差別在于對Dtij,k(t)的求解方法不同。在求解Dtij,k(t)時,Ant-Quantity模型、Ant-Density模型采用局部信息(即螞蟻完成一步便更新當前路徑上的信息素),而Ant-Cycle模型采用整體信息(即螞蟻完成一個循環后才更新所有路徑上的信息素)。Ant-Cycle模型更適用于求解TSP,因此本文采用Ant-Cycle模型來更新信息素。
對于Ant-Cycle模型:

式中Q——信息素強度
Lk——第五只螞蟻在本次循環中所走路徑的總長度
2.2 參數確定
蟻群算法中的a、b、r、m、Q等參數的設定尚無嚴格的理論依據,至今還沒有確定最優參數的一般方法,已公布的參數設置成果都是針對不同蟻群算法模型的。當采用Ant-Cycle模型時,理想的參數設定范圍為:0≤a≤5,0≤b≤5,0.1≤r≤0.99,10≤Q≤10000。
在面對具體問題時,可以按照段海濱[6]總結出的方法確定最優參數,具體步驟如下:第一步,確定m,按照

確定所需的螞蟻數量。第二步,調整設定范圍大的參數:a、b、Q。第三步,調整設定范圍小的參數:r。反復按照以上步驟進行調整,直至選擇出一組比較滿意的參數為止。
3 優化目標
引入當量費用長度概念,以環狀燃氣管網造價最低為目標,建立優化目標函數Lmin為:

式中Lmin——優化目標函數
lw,ij——當量費用長度,m
uij——判定系數
文獻[7—8]認為燃氣管網造價近似為管長的線性函數,基于這種理論,當量費用長度lw,ij的計算式為:
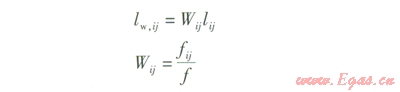
式中Wij——節點i與j路徑間管道的權系數
¦ij——燃氣管道在實際敷設方式下節點i與j路徑間管道單位管長造價,元/m
¦——燃氣管道在標準敷設方式下的單位管長造價,元/m
4 算例
選取某小型環狀燃氣管網(中壓)作為優化對象,氣源擬采用單氣源供氣。為了方便討論,進行以下設定:所有的節點間管道的權系數相等,且為1;只考慮形成單環狀管網。中壓管網的初步布置形式見圖l,節點4與氣源連接,各節點在二維坐標系中的坐標見表1。
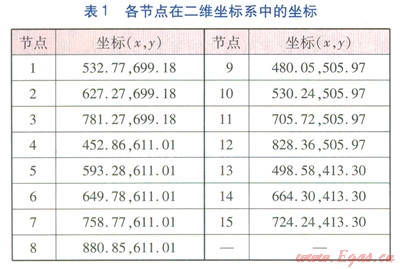
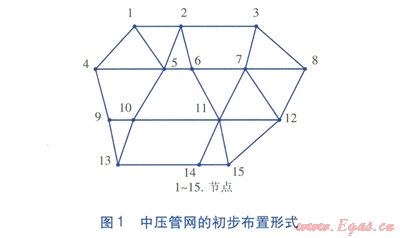
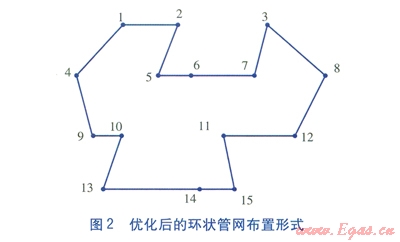
利用C語言編制蟻群算法程序,經過多次試算確定蟻群算法的參數為:m=15,a=1.0,b=5.0,r=0.1,Q=100。迭代最大次數為200,防止出現死循環。優化后的環狀管網布置形式見圖2,燃氣管網總長度為15.143km。
參考文獻:
[1]CHANG S K.The generation of minimal tree with a steiner topology[J].Journal of Association of Computing Machinery,1972(4):699-711.
[2]FLANIGN O.Constrained derivatives in natural gas pipeline system optimization[J].Journal of Petroleum Technology,1972(5):549-556.
[3]呂木英.基于遺傳算法的城市燃氣管網最優化布局研究(碩士學位論文)[D].武漢:武漢理工大學,2009:56-59.
[4]王垣,段常貴.改進遺傳算法在燃氣管網布局優化中的應用[J].哈爾濱工業大學學報,2006,38(1):46-48.
[5]SALZBORN B.Optimal design of gas pipeline networks[J].The Journal of the Operational Research Society,1979(12):1047-1060.
[6]段海濱.蟻群算法原理及其應用[M].北京:科學出版社,2005:34-36.
[7]劉洪,胡昌權,胡攀峰,等.用遺傳算法進行輸氣管網布置的優化設計研究[J].天然氣工業,2006,26(10):127-129.
[8]聶廷哲,段常貴.基于Hopfield神經網絡的輸氣管網布線優化[J].天然氣工業,2005,25(2):155-157.
本文作者:李自力 趙峰 李佳 楊立業
作者單位:中國石油大學(華東)儲運與建筑工程學院
武漢煉化工程設計有限責任公司
勝利油田勝利勘察設計研究院有限公司
您可以選擇一種方式贊助本站

支付寶轉賬贊助

微信轉賬贊助
